Derivada del cociente de 2 funciones

                  Formula para sacar la derivada:

para entender mejor te mostramos el siguiente video como EJEMPLO:

TRIÁNGULOS EQUILATEROS.

Pasos a seguir para formar un triangulo equilatero se le domina con este nombre por tener los 3 lados iguales.



ECUACIONES.

¿Como puedo saber si lo estoy haciendo es una ecuación en verdad?
Ejemplo: identificación de una ecuación
Don Juan al ir a pagar la reparación de su carro le presentaron la siguiente cuenta que estaba manchada de tinta ¿se podrá saber cuanto le cobraron de mano de obra a sr. Juan?

taller automotriz         "VELAZQUEZ"

cuenta de gastos de reparación modelo 5101

propietario : sr Juan

refacciones..........................................$985

mano de obra......................................$***

total....................................................$1115

para saber el costo de mano de obra, se plantea la siguiente situación

985+____=$1115

¿que numero sumado con 985 da como resultado 1115?

para contestar esta pregunta , se tiene que hacer una resta de l a forma siguiente :

1115  total 

985    reparaciones

____________

130     mano de obra

por lo tanto, se puede concluir que le cobraron $130 por mano de obra por que 985+130=1115

LAS EXPRESIONES COMO         985+***=1115 RECIBEN EL NOMBRE DE ECUACIONES

Considérese la ecuación X+37=82 en donde X es la incógnita

Para resolverla se resta 37 a sus 2 miembros y se tiene que:

X+(37-37)= 82-37

X+0=82-37

X=45

La solución de esta ecuación es 45 para probar esto se sustituye en X  el valor encontrado y se observa que efectivamente:

X +37=82

45+37=82

      82=82

LISTOOOOOOOO!!!!!!!!!!! ESTO YA QUEDO Y ERA MUY FÁCIL

ANGULOS

                                                  ÁNGULOS

Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.

Existen básicamente dos formas de definir un ángulo en el plano:

Forma geométrica: Se le llama "ángulo" a la amplitud entre dos líneas de cualquier tipo que concurren en un punto común llamado vértice. Coloquialmente, ángulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección.

Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una posición final. Si la rotación es en sentido levógiro (contrario a las manecillas del reloj), el ángulo se considera positivo. Si la rotación es en sentido dextrógiro (conforme a las manecillas del reloj), el ángulo se considera negativo.

Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, etc.

                           Clasificación de ángulos

Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:

.

Tipo	Descripción
Ángulo nulo	Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0°.
Ángulo agudo	Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de  rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100 g (grados centesimales).

Ángulo recto	Un ángulo recto es de amplitud igual a  rad Es equivalente a 90° sexagesimales (o 100g centesimales). Los dos lados de un ángulo recto son perpendiculares entre sí. La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
Ángulo obtuso	Un ángulo obtuso es aquel cuya amplitud es mayor a  rad y menor a  rad Mayor a 90° y menor a 180° sexagesimales (o más de 100 g y menos de 200 g centesimales).
Ángulo llano, extendido o colineal	El ángulo llano tiene una amplitud de  rad Equivalente a 180° sexagesimales (o 200 g centesimales).
Ángulo oblicuo	Ángulo que no es recto ni múltiplo de un ángulo recto. Los ángulos agudos y obtusos son ángulos oblicuos.

ÁNGULOS

EN EL CASO DE LOS ÁNGULOS NOTABLES SE DEMUESTRAN LOS TEOREMAS CON LOS QUE SE DEDUCEN LAS FORMULAS PARA CALCULAR SUS RESPECTIVAS MEDIDAS.

ANGULO CENTRAL

ES AQUEL QUE ESTA FORMADO POR DOS RADIOS.

EL <AOB INTERCEPTA O SUBTIENDE A LA CUERDA AB.

TAMBIÉN SE DICE QUE EL ARCO AB ESTA

COMPRENDIDO ENTRE LOS LADOS DEL ANGULO

ANGULO INSCRITO

ES AQUEL QUE ESTA FORMADO POR DOS CUERDAS Y TIENE SU VÉRTICE SOBRE LA CIRCUNFERENCIA. UN ANGULO ESTA INSCRITO EN UN ARCO, CUANDO TIENE SU VÉRTICE EN EL ARCO Y LOS LADOS PASAN POR LOS EXTREMOS DE ESTE. EL <B ES UN ANGULO INSCRITO, SUS LADOS SON LAS CUERDAS AB Y BC. EL <B ESTA INSCRITO EN EL ABC Y SUBTIENDE EL ARCO BC.

ANGULO INTERIOR

ES AQUEL QUE ESTA FORMADO POR DOS CUERDAS QUE SE CORTAN.

                                                                                                                    

EL <AEC,  (O BIEN SU OPUESTO POR EL VÉRTICE

<BED) ES UN ANGULO UNTERIOR DONDE EL ARCO AC Y BD SON LOS ARCOS COMPRENDIDOS ENTRE SUS LADOS. EL <AED (O BIEN SU OPUESTO POR EL VERTICE <BEC) ES UN ANGULO INTERIOR. AD Y BC SON CUERDAS COMPRENDIDOS ENTRE SUS LADOS.

ANGULO EXTERIOR

ES AQUEL QUE ESTA FORMADO POR DOS SECANTES QUE SE CORTAN EN UN PUNTO FUERA DEL CIRCULO.

¿para qué nos sirve la fórmula general?

PARA QUE NOS SIRVE LA FORMULA GENERAL

La formula general se puede usar para resolver cualquier ecuación de segundo grado

Por ejemplo, para resolver una ecuación como

 se hace de la siguiente

Manera.

1.      Se escribe la ecuación en su formula general

2.- se obtienen los valores de a, b, c

3.- En la formula se sustituyen, a, b, c por sus respectivos valores.

4.- se realizan las operaciones indicadas.

5.-se obtiene la solución.

6.- se verifica las soluciones en la ecuación original  

Moly : la trigonometria es una de las materias mas dificultosas que hay en las matematicas,dare de mi todo el conocimiento que tenga para que puedas solucionar tu problemas trigonometricas.

ecuaciones cuadraticas

Esto es una ecuación cuadrática:conoce¡

(a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.)

La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes

Ejemplos de ecuaciones cuadráticas:

		En esta a=2, b=5 y c=3
		Aquí hay una un poco más complicada: ¿Dónde está a? En realidad a=1, porque normalmente no escribimos "1x2" b=-3 ¿Y dónde está c? Bueno, c=0, así que no se ve.
		Esta no es una ecuación cuadrática, porque le falta el x2 (es decir a=0, y por eso no puede ser cuadrática)

¿Qué tienen de especial?

Las ecuaciones cuadráticas se pueden resolver usando una fórmula especial llamada fórmula cuadrática:

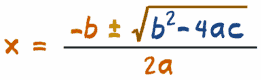
	El "±" quiere decir que tienes que hacer más Y menos, ¡así que normalmente hay dos soluciones!
	La parte azul (b2 - 4ac) se llama discriminante, porque sirve para "discriminar" (decidir) entre los tipos posibles de respuesta: si es positivo, hay DOS soluciones si es cero sólo hay UNA solución, y si es negativo hay dos soluciones que incluyen números imaginarios.

Solución

Para resolverla, sólo pon los valores de a,b y c en la fórmula cuadrática y haz los cálculos.

Ejemplo: resuelve 5x² + 6x + 1 = 0

Fórmula cuadrática: x = [ -b ± √(b²-4ac) ] / 2a

Los coeficientes son: a = 5, b = 6, c = 1

Sustituye a,b,c: x = [ -6 ± √(6²-4×5×1) ] / 2×5

Resuelve: x = [ -6 ± √(36-20) ]/10 = [ -6 ± √(16) ]/10 = ( -6 ± 4 )/10

Respuesta: x = -0.2 y -1

(Comprobación:

5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = FUNCIÓN CUADRÁTICA
Diremos que una función f es una función polifónica si existen números reales a0, a1, 
a2,......an tales que: 
 f(x) = anx
n
 + an-1x
n-1 + . . . . . + a2x
2
 + a1x + a0 
Ejemplo: f(x) = 5 x6
 + 137 x4
 – x3
 + 8 es f : R→R cuyo grado es 6. 
Vamos a estudiar ahora la función de grado 2. 
Definición: a la función polifónica de grado 2 se la denomina función cuadrática
La expresión general de la función cuadrática es: 
Donde a , b y c son números reales siendo a ≠ 0 
Su dominio es el conjunto R porque es el conjunto más amplio para el cual la fórmula tiene 
sentido. 
Su gráfica es una parábola. 
Los términos reciben estos nombres : 
 término lineal 
y = a.x
2
 + b.x + c
 término cuadrático término independiente 
A esta forma de expresar las función cuadrática se la llama polifónica. 
Si le damos diferentes valores a los coeficientes a , b y c obtenemos las fórmulas de 
distintas funciones cuadráticas. 
Por ejemplo: 
f(x) = 2 x2
 + x – 6 ; h(t) = 80 t – 5 t2
 ; g(x) = -x2
 + 7 ; s(t) = 2 función CUADRÁTICA
Diremos que una función f es una función polifónica si existen números reales a0, a1, 
a2,......an tales que: 
 f(x) = anx
n
 + an-1x
n-1 + . . . . . + a2x
2
 + a1x + a0 
Ejemplo: f(x) = 5 x6
 + 137 x4
 – x3
 + 8 es f : R→R cuyo grado es 6. 
Vamos a estudiar ahora la función de grado 2. 
Definición: a la función polifónica de grado 2 se la denomina función cuadrática
La expresión general de la función cuadrática es: 
Donde a , b y c son números reales siendo a ≠ 0 
Su dominio es el conjunto R porque es el conjunto más amplio para el cual la fórmula tiene 
sentido. 
Su gráfica es una parábola. 
Los términos reciben estos nombres : 
 término lineal 
y = a.x
2
 + b.x + c
 término cuadrático término independiente 
A esta forma de expresar las función cuadrática se la llama polifónica. 
Si le damos diferentes valores a los coeficientes a , b y c obtenemos las fórmulas de 
distintas funciones cuadráticas. 
Por ejemplo: 
f(x) = 2 x2
 + x – 6 ; h(t) = 80 t – 5 t2
 ; g(x) = -x2
 + 7 ; s(t) = 2 t2
 + t –3 
 + t –3 

5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0)

En álgebra, un binomio consta únicamente de dos términos, separados por un signo de más (+) o de menos (-). En otras palabras, es una expresión algebraica formada por la suma de dos monomios.

Ejemplos 

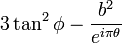 puede llamarse "binomio de razones trigonométricas".

Multiplicación de un número por un polinomio

Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.

3 · (2x³ − 3 x² + 4x − 2) = 6x³ − 9x² + 12x − 6

Multiplicación de un monomio por un polinomio

Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.

3x² · (2x³ − 3x² + 4x − 2) = 6x⁵ − 9x⁴ + 12x³ − 6x²

Multiplicación de polinomios

P(x) = 2x² − 3    Q(x) = 2x³ − 3x² + 4x

Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.

P(x) ·  Q(x) = (2x² − 3) · (2x³ − 3x² + 4x) =

= 4x⁵ − 6x⁴ + 8x³ − 6x³ + 9x² − 12x =

Se suman los monomios del mismo grado.

= 4x⁵ − 6x⁴ + 2x³ + 9x² − 12x

Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.